Introduction
Le traitement comptable des emprunts indivis suscite souvent des interrogations : comment calculer les remboursements par annuités constantes ?
Avec des implications financières majeures, il est essentiel de maîtriser cette méthode pour optimiser le choix de la modalité d'emprunt. Dans cet article, nous vous dévoilons toutes les clés nécessaires pour :
- calculer un tableau de remboursement d'emprunt ;
- enregistrer en comptabilité la réception des fonds et le remboursement des échéances.
Définition et principe de l'emprunt par annuités constantes
Qu'est-ce qu'un emprunt indivis ?
Un emprunt est une opération par laquelle une entité (entreprise, collectivité ou particulier) se finance en obtenant des ressources financières auprès d'un prêteur. Généralement, une banque ou des investisseurs, en s'engageant à rembourser le montant emprunté (le capital) assorti d'un intérêt, selon des modalités et un calendrier définis à l'avance.
Caractéristiques principales
- Montant et durée : L'emprunteur reçoit une somme dont il devra disposer et rembourser sur une période déterminée.
- Intérêts : En contrepartie de l'usage des fonds, l'emprunteur verse des intérêts, lesquels représentent le coût du financement.
- Garanties : Un emprunt peut être assorti de garanties (hypothèques, cautionnements, nantissements) qui sécurisent le prêteur en cas de défaillance de l'emprunteur.
- Modalités de remboursement : Le remboursement peut se faire en une seule fois (ballon) ou de manière échelonnée (amortissement constant et annuité constante).
Le principe des annuités constantes
Le remboursement par annuités constantes signifie que l'emprunteur rembourse le prêt via des versements périodiques et constants pendant toute la durée de l'emprunt. Chaque annuité comprend une partie du capital plus les intérêts accumulés. Le principal avantage de cette méthode est sa prévisibilité financière, permettant aux emprunteurs de planifier leurs finances efficacement.
Calcul des annuités constantes
Pour déterminer le montant de chaque annuité, vous devez tenir compte de la somme empruntée ("C"), du taux d'intérêt pour la période (annuel en général, "i") et de la durée totale de l'emprunt ("n"). La formule pour calculer chaque paiement est la suivante :
Annuité = C * (i/(1+i)^-n)
C : Capital emprunté
i : est le taux d'intérêt par période
n : est le nombre total de périodes.
Le tableau de remboursement d'emprunt

- Capital restant dû en début de période : Il s’agit du montant initial de l’emprunt pour la première échéance et, pour les périodes suivantes, du capital non remboursé à la fin de l’échéance précédente ;
- Intérêts : Ils se calculent en appliquant le taux d’intérêt au capital restant dû en début de période, représentant le coût de l’emprunt pour l'échéance considérée.
- Amortissement du capital : Ce montant correspond au remboursement effectif du capital, obtenu en soustrayant les intérêts de l’annuité constante « A ».
- Annuité : Notée « A », elle est fixe et regroupe, pour chaque échéance, la somme des intérêts et de l’amortissement du capital.
- Capital restant dû en fin de période : Ce montant s’obtient en déduisant l’amortissement du capital du capital initial de la période.
Enregistrement comptable de l'emprunt
En comptabilité, un emprunt est inscrit au passif du bilan de l'emprunteur. Chaque période, un remboursement du capital et/ou des intérêts doit être effectué par l'entité.
Les intérêts courus non échus, sont enregistrés dans le compte de charges financières à la clôture de l'exercice, afin de respecter le principe d'indépendance des exercices.
Souscription de l'emprunt
Au moment de la contraction de l'emprunt, l'écriture comptable consiste à débiter le compte 512 - Banque et à créditer le compte 164 - Emprunts auprès des établissements de crédit.

Remboursements à l'échéance
Pour chaque annuité payée, il convient de débiter le compte 164 - Emprunts auprès des établissements de crédit pour la partie capital remboursée, le compte 661 - Charges financières pour les intérêts, et de créditer le compte 512 - Banque. Cela reflète la diminution de la dette au fil du temps.

Exemple d'emprunt remboursable par annuité constante
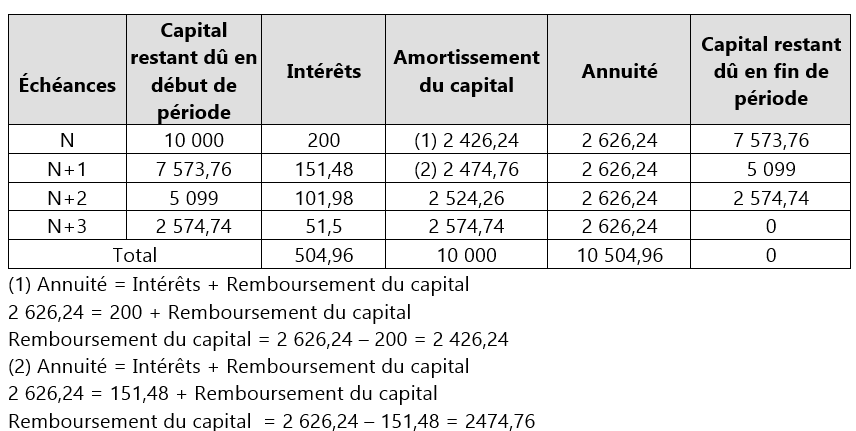
Exemple : L’entreprise souscrit un emprunt de 10 000 €. Le remboursement est effectué par annuités constantes sur une durée de 4 ans. Le taux d’intérêt annuel est de 2 % et les intérêts sont payés annuellement en.
Annuité = 10 000 * ((0,02/(1-(1+0,02)^-4)) = 2 626,24 €
Implications financières et fiscales
En optant pour un remboursement par annuités constantes, il est important de comprendre les implications tant sur le plan du reporting financier que sur celui de la fiscalité. En effet, le ratio du service de la dette affecte la liquidité et le bilan de l'entreprise.
Avantages du remboursement par annuités constantes
Le principal avantage de cette méthode de remboursement réside dans la simplicité de la gestion des flux de trésorerie, grâce à des paiements réguliers et prévisibles. Cela permet une gestion financière plus aisée et une meilleure planification. Avec des paiements uniformes, la gestion comptable est simplifiée. Les entreprises et les particuliers peuvent intégrer ces paiements réguliers dans leurs prévisions financières sans avoir à recalculer les montants dus à chaque période. Cette uniformité réduit également le risque d'erreurs dans les enregistrements financiers.
Conclusion
Maîtriser le traitement comptable et le calcul des emprunts indivis avec remboursement par annuités constantes est essentiel pour une gestion financière optimale. En comprenant les principes et en appliquant les bonnes méthodes, vous pouvez planifier efficacement vos remboursements et optimiser vos finances.


